ليست مجرد أرقام وحسابات ولا حتى مساحات، النظريات الرياضية جزء من حياتنا!

توصّلنا في المقال السابق عن طبيعة الرياضيّات هل هي اكتشافٌ أم اختراع، إلى أنّ الرياضيّات موجودة منذ الأزل، لدرجة أنّ الديناصورات قد اكتشفتها متأخّرةً جدًا، وقلنا طالما الأمر هكذا فأين هي الرياضيات من حولنا؟
أوّلًا، علينا استيعاب صفة غاية في الأهمّيّة من صفات الرياضيّات وهي المثاليّة المطلقة، بينما العالم من حولنا يختلف قليلًا، فحيث أنّ إجابة أيّ سؤال يصادفنا في الرياضيّات ستكون إمّا خاطئة أو صحيحة، فإنّ الحياة تمنحنا الكثير من المساحة لنراوِح فيها، وقد تعلّمنا أنّه لا يمكن تصنيف كلّ ما حولنا على أنّه إما صحيح أو خاطئ، فالترتيب الظاهري للأحداث في محيطنا هو متوسّط نتائج ملايين الحوادث الصغيرة والتي تتّصف غالبيّتها بالعشوائيّة، وهنا تأبى الرياضيات رغم مثاليّتها أن تتركنا تائهين في هذا المحيط المليء بأحداثٍ عشوائيّة، بل ربّما كانت المثاليّة هي الدافع لتمسك الرياضيّات بزمام الأمور وينشأ لدينا فرعٌ واسع من فروع الرياضيات وهو الاحتمال.
لا يمكن أن يمرّ يومٌ دون استخدامنا للاحتمال والاعتماد على نتائج احتماليّة، ولا أقصد استخدامنا لكلمة “احتمال” ومشتقّاتها، بل أقصد الاحتمال الرياضيّ بحدّ ذاته، فإمّا أن تراقب الطقس أو تراقب أسعار الأسهم أو سعر عملةٍ ما أو تسمع خبرًا عن دواءٍ ما وكلّ هذه الحوادث تعتمد بشكلٍ أساسي على استخدام الاحتمال بشكلٍ خاصّ والرياضيات عمومًا.
الاحتمالات أبسط الأشياء
بالرغم من استخدامنا شبه اليومي لمفاهيم الاحتمال، والتي تتعلّق مباشرةً بفرع واسع جدًا من الرياضيات هو الإحصاء، والذي يجاهد الاقتصاديّون لجعله فرعًا من فروع الاقتصاد، بينما يحاول بعض الإحصائيين الانشقاق عن الرياضيّات والادّعاء بأنّ الإحصاء علمٌ مستقلّ، مع ذلك ومهما كانت نتيجة هذا الصراع النظريّ، فإنّ مفاهيم الإحصاء والاحتمال هي مفاهيم رياضيّة وهنا تسجّل الرياضيّات نقطة حضور لمن يسأل أين نجد الرياضيّات.
يسرّني أن أخبركم بأنّ كلّ ما سبق نقطة في بحر الآتي، هل سمعتم بفرع اسمه “نظريّة البيان” Graph Theory وهي تدرس خواصّ المخطّطات البيانيّة، حيث تُمَثَّل مجموعة من الكائنات المترابطة بعلاقاتٍ ما بنقاط، تصل بين هذه النقاط خطوط أو أسهم.
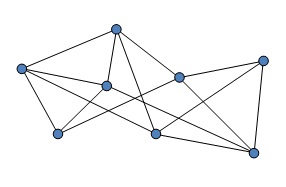
نشأة نظرية البيان
كانت البداية على يدّ الرياضيّ المبدع أويلر 1736 الذي وضع نهايةً لمسألة تسمى مسألة جسور كونيغسبرغ والتي أثبت فيها أنّ حلّ تلك المسألة مستحيل وهي باختصار أنّ قرية كونيغسبرغ تحوي عدة جسور وجزر في النهر، والمطلوب المرور على كل الجسور مرة واحدة دون تكرار، من الواضح أنّ البداية كانت للتسلية وهذا ما تكلّمنا عنه في مقال “أهمية الرياضيات البحتة“، واستمرّت التسلية لزمنٍ طويل، وابتُكرت مسائل عديدة مثل مسألة الحصان في رقعة الشطرنج والذي يجب أن يمرّ على جميع الخانات في الرقعة دون تكرار، ثمّ واحدة من أهمّ المسائل في تاريخ الرياضيّات والتي لم تُحلّ حتى اليوم وهي مسألة البائع المتجوّل.
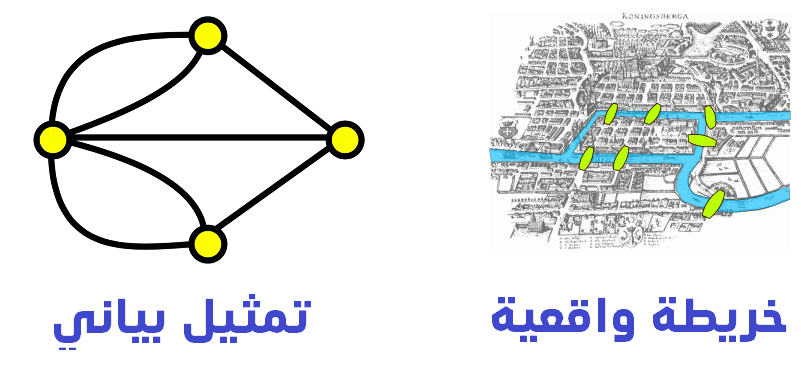
اليوم تُدرس نظرية البيان من قبل علماء الرياضيات وعلماء الكمبيوتر، ولديها تطبيقات مثيرة للاهتمام، مثلًا فيسبوك هو في الأساس رسم بياني ضخم واحد، فيمكن اعتبار كل مستخدم “نقطة”، تتصلّ بخطوط مع نقاط أخرى، تمثّل كلّ منها صديقًا، والخطّ هو علاقة الصداقة، يسمح هذا التجريد الرياضي لفيسبوك بالقيام بأشياء مثل إظهار الاتصالات من الدرجة الثانية (أصدقاء الأصدقاء).
كما تعد الرسوم البيانية (داخل نظرية البيان وليست تلك المستخدمة في التفاضل والتكامل) أيضًا طريقة مفيدة لتنظيم أشياء مثل تطبيقات GPS، حيث تسمح لك عند تحويل الخريطة إلى نقاط وخطوط بالعثور على أقصر مسار على طريق بين نقطتين داخل مدينة مكتظة بالأبنية، وهو ما بات يُعرف فيما بعد بـ “هندسة سيارة الأجرة“، حيث تضطرّ هناك للتخلّي عن واحدة من بديهيّات الرياضيّات التي تعلّمناها في المرحلة الابتدائية وهي أنّ أقصر مسار بين نقطتين هو الخطّ المستقيم، حيث من الممكن أن يصبح مضلعًا أو منحنيًا.
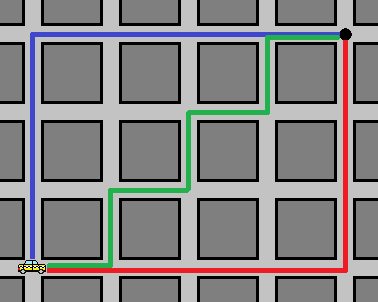
نوعٌ آخر من الهندسات
بطريقةٍ أو بأخرى سنجد أنفسنا في أحد التطبيقات الحاسوبية كلّما بحثنا عن تطبيقات رياضيّة، وهذه المرّة مع “الهندسة الوصفيّة“، هذا القسم المنسي من الرياضيّات، والذي يعرفه جيّدًا طلّاب كلّيّات الهندسة ومعاهدها، كما أنّهم يصنّفون هذه المادّة كأصعب الموادّ الدراسية، وذلك لاعتمادها على المساقط متعدّدة الاتّجاهات، والطريف أنّ مؤسّس هذا الفرع من الرياضيات هو غاسبار مونج ذاته مؤسس مدرسة الفنون التطبيقية في باريس، وشأنه شأن نيوتن الذي أسس فرع التفاضل والتكامل كأثر جانبي لدراسته في الفيزياء النظرية، كانت الهندسة الوصفية ناتجًا جانبيًا لعمل مونج في تدريس الفنون حيث كان بحاجة ماسّة في نهاية القرن الثامن عشر لطريقة فعّالة لنقل الأشكال ثلاثيّة الأبعاد إلى الورق ذي البعدين.
اليوم لم يعد المهندسون بحاجة ماسّة لممارسة هذا النوع من الأعمال لأنّ الحواسيب تقوم بالمهام على أكمل وجه، لكن مبدأ عملها قائم على ما أسّسه مونج، ليس هذا فحسب بل إنّ كلّ ما تراه على الشاشات التي تحيط بك من كلّ جانب تعتمد بشكلٍ رئيس على الهندسة الوصفية التي تُدعى أحيانًا الهندسة الإسقاطيّة، فبفضلها نحن اليوم نشاهد على شاشاتنا المسطّحة أشكالًا لا نشكّ أبدًا بأنّها ثلاثيّة الأبعاد.
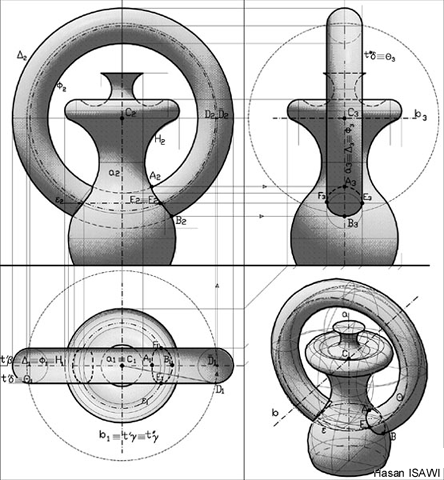
جميعنا نعرف الثورة التي أحدثتها الطابعات ثلاثية الأبعاد، وهذه أحد تطبيقات الهندسة الوصفية لكن بشكلٍ معاكس، حيث تعيد تشكيل المساقط ثنائية الأبعاد لتنتج منها أشكالًا مجسّمة، وذلك بعمليّة تبدو بسيطة فما على المستخدم إلا تزويد البرنامج بصور (ثنائية البعد) يلتقطها بكاميرا هاتفه، من كافّة الاتّجاهات، وسيتولّى الحاسوب تحويلها عبر سلسلة من الإسقاطات إلى تمثيلٍ تستطيع الطابعة ترجمته إلى منحوتة مجسّمة.
لو أردنا سرد المجالات التي تدخّلت فيها الرياضيات بشكلٍ مباشر أو غير مباشر فلن ننتهي أبدًا، لكن اخترتُ المواضيع السابقة لأنّها ذات أثرٍ كبير ويوميّ ومع ذلك فهي منسيّة، وهذا ممّا قد يُشعر المشتغلين بها بالغيظ، بسبب عدم تقدير أعمالهم، مع ذلك فإنّ هناك العديد من المواضيع التي تجعل الرياضي يبكي، والتي قد أفرِدُ لها مقالًا خاصًا.





تعليق واحد