ما هي الهندسات اللاإقليدية
تنقسم الهندسات غير الاقليدية الى عائلتين كبيرتين: الأولى هي الهندسة الاهليليجة elleptic geometry واللتى يطلق عليها احيانا هندسة ريمان Rieman Geometry و هي تتميز بأن مجموع زوايا المثلث فيها اكبر من 180 درجة. اما العائلة الثانية فهى الهندسة القطع زائدية او hyperbolic geometry ويطلق عليها احيانا هندسة لوباتشيفسكى Lobatchevskian geometry وهي تتميز بان مجموع زوايا المثلث فيها أقل من 180 درجة. وطبعا العلامة المميزة للهندسة الاقليدية نفسها هي ان مجموع زوايا المثلث يساوى فيها 180 درجة تماما.
وللتنوية فإنّ هذا موضوع ليس بحثاً أكاديمياً يغطي الهندسات غير الاقليدية فهناك على الأقل سببان يحولان دون ذلك. اولهما ضيق المساحة. فسرد برهان واحد قد يحتاج مساحة تكافئ مساحة مدونة اليوم او اقل او اكثر قليلا! اما السبب الثانى فهو اننا لانملك الأدوات الكافية لذلك. ففى حين ان الهندسة الاقليدية بديهية و ادواتها بسيطة لذلك يتعلمها تلاميذ الصف الأول أو الثانى الأبتدائي بلا مشاكل. نجد أن الأدوات اللتى تحتاجها الهندسة غير التقليدية اكثر كلفة. فالحد الأدنى لذلك هو معرفة قوية بالمنطق الرياضى ونظرية المجموعات! مع ذلك فإننا نهدف اليوم إلى أمرٍ عميق! اننا نهدف الى الوصول الي روح و فلسفة الهندسات غير الاقليدية. والامر اشبه بلعبة كرة القدم . فانا قد اشاهد مباراة لكرة القدم و افهمها مع انى قد لا استطيع ان امارسها! وتبقى ممارسة كرة القدم مقصورة على لاعبين ذوي قدرات بدنية مميزة وان كان يشعر المرء احيانا ان بعض اللاعبين المحترفين ينقصهم الفكر الكروي لما يفعلونه!
الهندسة الكروية
إن دراسة خواص الأشكال الهندسية على سطح كرة هى احد افرع الهندسة الفراغية الهامة. وهى معروفة منذ امد بعيد فقد كانت مفيدة فى دراسة الفلك حيث درس الانسان مواقع النجوم على قبة السماء. كما انها ضرورية فى قياسات المساحة بسبب سطح الأرض الكروي. لكن هنا يلوح تساؤل: الكرة نفسها جسم ثلاثى الأبعاد اما سطحها فهو ثنائى الابعاد فقط. فقيمة خطي الطول و العرض كافيتان تماما لتحديد موضع اى بقعة على وجه الأرض. لكننا لا نستطيع ان نتعامل مع سطح الأرض المقوس فى ضوء هندسة اقليدس المستوية. فقط نستطيع ان نتعامل معه فى ضوء هندسة اقليدس القراغية الثلاثية الابعاد. السؤال الأن: هل يمكننا ان نجد طريقة نتعامل بها مع سطح الكرة الثنائي الأبعاد أساسا من خلال بعدين فقط؟

دعونا نتخيل كرة ونقطتين مختلفتين تقعان على سطحها. ودعونا نقيم خطا مستقيما يصل بينهما. سنجد ان هذا الخط يقع بالكامل باستثناء النقطتين السابقتين خارج سطح الكرة. وكما نعلم فان هندسة اقليدس قائمة على دراسة خواص الخطوط المستقيمة بالنسبة لبعضها. اذن هندسة اقليدس لن تنفعنا ابدا فى الوصول الى هدفنا اللذى اشرنا اليه. فلا وجود للخطوط المستقيمة من البداية على سطح الكرة. ولا حتى بامكاننا استعمالها كخطوط مساعدة. اذن فأى محاولة للاعتماد على الهندسة الأقليدية فى دراسة خواص سطح الكرة بدلالة بعدين هى كاقامة دورة توعية لعمل التنفس الصناعى لطائر البطريق المار فى الصحراء!
ثم دعونا نتأمل فى ماهية الخط المستقيم. فحسب التعريف الرابع لاقليدس فى كتاب العناصر فان:
“المستقيم هو خط يتطابق مع استواء النقاط اللتى تقع فوقه”
وفى الحقيقة وبالرغم من اننى بحثت فى مصادر عديدة وبلغات مختلفة عن صياغات مختلفة لهذا التعريف -كما التعريف السابع ايضا- فلم اجد نصا يرضينى. فانا لا افهم ماذا يقصد اقليدس من تعريفه هذا. وأقصى ما يفهمه المرء ان هناك نوع من الخطوط اسمه الخط المستقيم ! فمشكلة تعريفات اقليدس انها تعتمد على بداهة المستقبل بشكل كبير. واقليدس يعتمد على ان جميع الناس عندما يسمعون لفظ الخط المستقيم يقفز فى مخيلتهم نفس الشكل تماما. لكن هذه الطريقة ليست صحيحة بمعايير رياضيات اليوم. ولكن دعونا نتخطى هذه النقطة و نفترض ان الشكل الذى تتصوره انت وانا حول الخط المستقيم يتطابقان تماما. لكن وكما تري فان هذا الشكل ليس من القاطنين على سطح الكرة و لايمكننا توطينه هناك ابدا.

إذاً ما هى الخاصية الثانية من خواص الخط المستقيم -بخلاف شكله البديهي- التى ربما قد نستطيع توفيرها على سطح الكرة؟ تقول النظرية العشرون فى كتاب العناصر ان الخط المستقيم هو أقصر مسار يصل بين نقطتين. او بمعنى ادق طول اى ضلع فى مثلث اصغر من مجموع الضلعين الاخرين. فلو تخيلنا مرة اخرى نقطتين على سطح الكرة فما هو اقصر مسار يصل بينهما؟ الاجابة انها الدائرة العظمى! حيث الدائرة العظمى هى اكبر دائرة يمكن رسمها على سطح الكرة وهي تشترك مع الكرة فى نفس المركز وطول نصف القطر. وعلى سبيل المثال فإن جميع خطوط الطول فوق سطح الكرة الأرضية هى دوائر عظمي. وخط الاستواء فقط دونا عن باقى خطوط العرض الأخرى هو دائرة عظمى. وهذه الخطوط نطلق عليها الخطوط الجيوديسية geodesic . لكن هل نستطيع ان نقيم من خلالها هندسة مترابطة؟ الأحابة هى نعم وسنحصل فى المطلق على نفس النتائج اللتى نحصل عليها فى ضوء الهندسة الفراغية! وأرجو الانتباه الى كلمة المطلق!
لكن دعونا اولا نرى كيف تتوافق الهندسة الكروية الجديدة مع مسلمات اقليدس الخمسة. تقول المسلمة الاولى انه بامكاننا ان نرسم خطا وحيدا يمر بين نقطتين مختلفتين. لكن هذه المسلمة لن تصمد فى الهندسة الكروية فمثلا نقطتا القطبين الشمالى والجنوبى يمكننا ان نصل بينهما بعدد لانهائى من الخطوط وهى خطوط الطول!
وماذا عن المسلمة الثانية التى تقول انه بامكاننا مد اى قطعة مسقيمة من كلا طرفيها؟ اذا نظرنا مثلا الى اى خط طول معين واخذنا نقطتين عليه فالنقاط بينهما تمثل القطعة المستقيمة. ثم من كلا النقطتين نستطع ان نسير الى مالانهاية. فالدائرة العظمى صحيىح انها شكل منتهى ولكنها بلا حدود. ونحن نستطيع ان نمشى فوق سطح الكرة الارضية الى مالانهاية بدون ان نصل الى حافة العالم. فهذه المسلمة متحققة لفظيا! وان كان اقليدس على الأغلب لم يقصد ذلك المعنى.
اما المسلمة الثالثة فهى تقول بانه بامكاننا رسم اى دائرة من اى مركز وبأى نصف قطر. وطبعا يمكننا رسم دوائر على سطح الكرة من اى نقطة فوقها. لكن ما المقصود بأى نصف قطر؟ فنحن نعلم ان الكرة جسم منتهى. فاذا كان المقصود بطول نصف القطر هو اى قيمة مطلقة فلن تتحقق هذه المسلمة فهناك حد اقصى لنصف قطر الدوائر الممكن رسمها. اما اذا كان المقصود باي نصف القطر هو اننا بواسطة اى نقطتين فوق سطح الكرة نستطيع رسم دائرة بحيت تكون احد النقطتن مركزها بينما تقع النقطة الاخرى على محيطها فستكون هذه المسلمة متحققة.
اما المسلمة الرابعة والتى تفيد بتساوي جميع الزوايا القائمة فهى سارية هنا ايضا.
ثم نصل الى المسلمة الخامسة الشهيرة. ودعونا نتعامل معها من خلال صياغة بلاي فير التى تقول انه من خلال اى نقطة تقع خارج خط مستقيم يمكننا رسم خط مستقيم واحد مواز للخط الاول. ولكننا كما نرى ان هذه المسلمة لن تتحقق. ففى عالم الهندسة الكروية لا توجد خطوط متوازية على الأطلاق. واى خط مستقيم يقطع اى خط مستقيم اخر فى نقطتين. وبامكانكم مرة اخرى ان تنظروا الى خطوط الطول اللتى تتقاطع كلها عند القطبين الشمالى والجنوبى. او الى خط الاستواء الذى يقطع جميع خطوط الطول فى نقطتين.

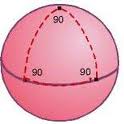
والأن ماذا عن الأشكال الهندسية الأساسية كالمثلثات؟ وكما نعلم فان المثلث هو شكل يتكون من 3 اضلاع تصل بين 3 نقاط لا تقع على خط واحد. ونرى فى الرسم مثلث اضلاعه هى خط الاستواء وخط جرينتش بالأضافة الى خط الطول 90 شرقا. وكما نرى فان مجموع زوايا المثلث الداخلية تساوى 270 درجة تماما! و القاعدة العامة تقول ان مجموع زوايا المثلث فى الهندسة الكروية دائما اكبر من 180 درجة! بل توجد فى الهندسة الكروية خاصية غريبة لا توجد فى الهندسة الاقليدية. حيث اننا فى ضوء الهندسة الأقليدية اذا علمنا قيمة زوايا المثلث الثلاثة فلن نستطيع ان نحسب مساحته. ونحتاج الى طول ضلع واحد على الأقل. اما فى الهندسة الغير اقليدية فاننا اذا علمنا قيمة الثلاث زوايا فباماكاننا حساب مساحة المثلث! وتكون مساحة المثلث هى الفرق بين مجموع زوايا المثلث بوحدة الراديان و الثابت π مضروبا فى مربع نصف قطر الكرة
الهندسة المطلقة
لقد رأينا توا احد انواع الهندسات الغير اقليدية التى لا تخالف المسلمة الأقليدية الخامسة فقط بل الاولى ايضا. وربما الثانية و الثالثة كما رأينا. ويصنف الرياضيون الهندسات الى مطلقة absolute geometry وغير مطلقة. وفى الهندسات المطلقة تتحقق المسلمات الأقليدية الاربعة الاولى. فقط المسلمة الخامسة ليست شرطا لها. بالمثل فى الشعر الكلاسيكى لا بد ان يحافظ الشاعر على شكل البيت و القافية. ثم هناك الشعر الحر اللذى لا يلتزم بتلك القيود. لكن هناك بعض الشعراء اللذين يقولون علينا ان نلتزم بالقافية حتى ولو نلتزم بشكل البيت التقليدي. فالهندسات المطلقة هى كذلك!

وفى الهندسة الكروية يمر بين نقطتي القطبين عدد لانهائي من الخطوط الجيوديسية. لكن الأمر ليس خاص بالقطبين فقط. ولكن نفس الامر يتكرر بالنسبة لاى نقطتين قطريتين. ولو فكرنا فى نموذج يعالج هذه المشكلة فدعونا نتخلص من نصف نقاط الكرة. بان نتخلى مثلا عن نصف الكرة الشمالى. ففى هذه الحالة ستبقي نصف الدوائر العظمى تمثل اقصر مسارا بين نقطتين. ويكون بامكاننا رسم خط جيوديسى واحد بين اى نقطتين مختلفتين. لكن المشكلة هنا ان المسلمة الثانية سوف يتم الاخلال بها. فهنا لن يمكننا مد الخطوط الى مالانهاية. فلهذا الشكل حافة وعندما نصل الى خط الاستواء لن يمكننا الوصول ابعد من ذلك!
وهنا يفترض نموذج الهندسة الأهيليجية فرض عجيب فيقول ان اى نقطتين قطرتين على خط الاستواء هما فى حقيقة الامر صورتان لنقطة واحدة. وهما وجهان لنفس العملة! فعندما يصل الخط الى الحافة عند خط الاستواء فانه يقفز فجأة الى الجانب الآخر ثم يواصل مسيرته. وهناك نموذج آخر يفترض نفس هذا التصور بالنسبة للكرة كاملة وليس فقط لنصف الكرة.بحيث تكون أى نقطتين قطريتين هما نفس النقطة. لكن دعونا نبقى فى نموذج نصف الكرة.

ودعونا الآن نتخيل اننا فصلنا خط الاستواء عن نصف الكرة الجنوبي فسيبدو كحزام دائرى. فاذا قمنا بعصر هذا الحزام حول احد قطريه تماما كما قد نعصر الملابس المبللة بالماء. فستنشأ عندنا بدلا من الدائرة حلقتان. ثم نقوم بثنى احد هذه الحلقات فوق الاخرى. فسنجد ان كل نقطتين كانتا فى البداية قطريتين تنطبقان الان فوق بعضهما. وهكذا هو الحال تقريبا فى النموذج الجديد.
دعونا الان نحاول ان نعيد نفس المحاولة ولكننا مع ابقاء خط الاستواء متصلا مع نصف الكرة الجنوبى. سنجد اننا لن نستطيع ان نقوم بذلك فى فضاء اقليدى ثلاثى الأبعاد. فلذلك نحتاج فضاء ذا أربعة ابعاد! اذن فكما امكننا تمثيل الهندسة الكروية الغير اقليدية ثنائية الايعاد من خلال فضاء اقليدي ثلاثي الابعاد نجد ان الهندسة الأهليليجية ثنائية الابعاد تحتاج حتى الى اكثر من 3 ابعاد اقليدية حتى يمكن تصورها!
الهندسة القطع زائدية

وهذه الهندسة هى طبعا هندسة غير اقليدية ولكنها على النقيض من الهندسة الإهليليجية. فلو تخيلنا سطحا لانهائيا يشبه سرج الحصان او رقائق البطاطس -الشيبسى-. ولو تخيلنا اننا غزلنا مفرشا على هذا الشكل فاننا لن نجد فيه خيطا مستقيما واحدا!! ومرة اخرى حيث انه لاتوجد خطوط مستقيمة فلا يمكن لهندسة اقليدس ان تصف هذا العالم ويكون المكافئ للخط المسقيم هو الخيط الذى له اقصر طول يصل بين نقطتين. وعلى هذا المفرش يمكننا رسم عدد لانهائى من الخطوط الموازية لخط اخر من نقطة خارجة عنه. واذا رسمنا مثلث سنجد ان مجموع زواياه يقل عن 180 درجة. وكلما كبرت مساحة هذا المثلث كلما زاد هذ الفرق. وحيث ان الفرق لا يمكن ان يصل الى 180 درجة سنجد ان هناك نهاية لمساحة اى مثلث مهما كبر. وتوصل لامبرت الى نتيجة عجيية وهي ان هندسة هذا العالم تكافئ الهندسة على سطح كرة ذات نصف قطر عبارة عن عدد تخيلي.

ثم استطاع الرياضى الايطالى بلترامي من تطوير اكثر من نموذج لإسقاط الهندسة القطع زائدية على الهندسة الاقليدية وسنستعرض سريعا واحدا فقط. وهذا النموذج يعرف باسم قرص بوان كاري Poincaré disk.
وفي هذا النموذج يتم التعبير عن المستوي الغير اقليدى اللانهائى فى صورة قرص أو دائرة وبحيث يمثل محيط هذا القرص المالانهاية. اى اننا عمليا لا يمكن ان نصل الى حافة القرص عندما نكون فى العالم الغير اقليدي. ويتم التعبير عن الخطوط الغير اقليدية المستقيمة اما فى صورة اقواس دائرية تصنع زاوية قائمة عند التقائها مع محيط القرص أو فى صورة خطوط قطرية. وكما فى الرسم فان الخط القطري الرأسى يمثل خطاً فى المستوى الغير اقليدى وباقى الاقواس هى ايضا خطوطا فى المستوى الغير اقليدي موازية للخط الأول. وينبغى ان نلاحظ ان معنى ان خطين متوازيان هما انهما لا يلتقيان.
ومن خواص هذا النموذج انه يحافظ على قيمة الزوايا فتبقى كما هى فى المستويين الاقليدي و الغير اقليدي. ولذلك يسمى ذلك النموذج conformal لكن الاطوال لا تحافظ على قيمتها. فالاطوال تبدو وكأنها تنسحق عندما تبتعد عن المركز وتقترب من محيط القرص. فانسان طول 1.8 متر مستلقى عند مركز القرص او بعيدا عنه سيبدو بنفس الطول عندما نقيسه فى المستوى الغير اقليدى. بينما اذا قسنا طوله طبقا لنموذج بوان كاري سيبدو عند المركز اطول منه عند الاطرف.ويمكننا تحويل الى الطول الغير اقليدى من هذا النموذج طبقا للمعادلة التالية

AB = ln(PA*QB/PB*QA) 1
الخاتمة
ولقد استطاع الرياضي ريمان التوحيد بين كل الهندسات السابقة لينتج الهندسة التفاضلية differential geometry. فنحن حتى الان لم نتعرض لكيفية حساب طول الخط فى الهندسات المختلفة او كيفية حساب انحناء مستوى ما. وهذه كلها اشياء ممكن حسابها فى الهندسات الغير اقليدية لكن باستخدام عمليات رياضية اكثر تعقيدا مثل التكامل وحساب الموترات.
كما نرى فى النهاية ان كل من الهندسات الاقليدية و الغير اقليدية هى هندسات مبرهنة منطقيا. ولذلك فكلها صحيحة. و الاعتقاد بان احدها صحيح والاخر خطأ انطلاقا من الاسماء هو كمن يعتقد ان الأعداد النسبية خاطئة لوجود الأعداد الغير نسبية. او اما ان الاعداد الحقيقية أو غير الحقيقية موجودة فقط! لكن يبقى السؤال اى هذه الهندسة هى الأجدر على وصف كوننا اللذى نعيش فيه؟
المصدر روائع العلوم



