كم مرة في اليوم يتعامد عقرب الدقائق مع عقرب الساعات؟
حساب كم مرة يتعامد عقربا الساعة خلال 12 ساعة

في كلّ دقيقة يتحرّك عقرب الدقائق 6 درجات، ويتحرّك عقرب الساعات نصف درجة.
وهذا واضح لأنّ عقرب الدقائق ينجز دورة كاملة (360 درجة) خلال ساعة كاملة أي 60 دقيقة، بينما يستغرق عقرب الساعات 12 ساعة أي 720 دقيقة لإنجاز دورة كاملة.
النقطة الأهمّ في حلّ هذه المسألة هي إدراك التالي:
للوهلة الأولى نعتقد أنّ أيّ زاوية بين عقربي الساعات والدقائق ستتكرّر كلّما دار عقرب الدقائق نصف دورة أي 180 درجة، مثلًا تكون الساعة 3:00 والزاوية 90 درجة، يظنّ الشخص المتعجّل أنّ الساعة 3:30 أي بعدما دار عقرب الدقائق نصف دورة وانقلبت الزاوية من الأعلى إلى الأسفل، ستصنع عندها العقارب زاوية 90 درجة للمرة الثانية، لكن نسي أنّ عقرب الساعات قد تحرّك خلال هذه النصف ساعة 15 درجة بالتالي الزاوية عند الساعة 3:30 ستكون 75 درجة، ونحن بحاجة لـ15 درجة إضافية حتى نصل إلى 90.
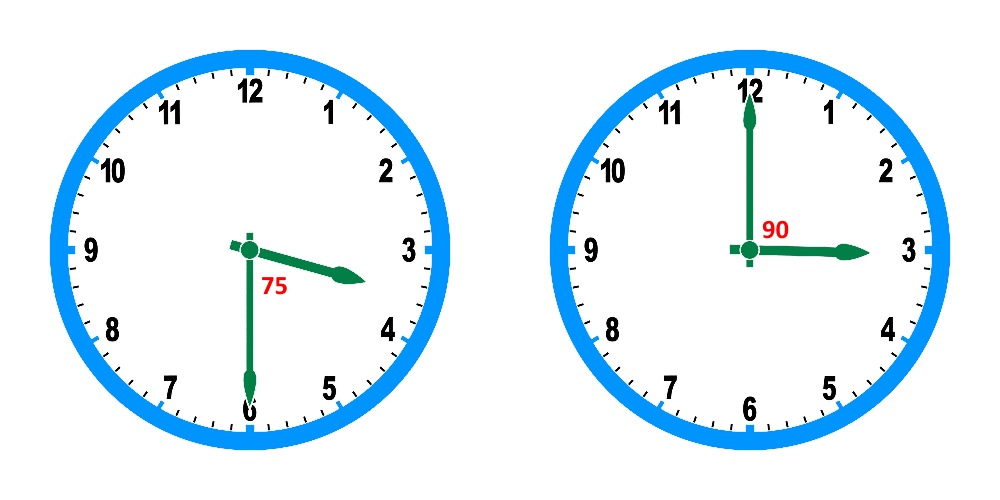
هنا تنشأ مشكلة جديدة، وهي أنّنا ببساطة يمكن أن ننتظر عقرب الدقائق ليتحرّك 15 درجة وهذا ما يستغرق دقيقتين ونصف، المشكلة هي أنّ عقرب الساعات لم يبقَ في مكانه بل تحرّك بدوره درجة وربع الدرجة، مرّة جديدة علينا منح عقرب الدقائق عدّة ثوان كي يعوّض النقص، والذي سيخلص نقصًا جديدًا أصغر هذه المرّة بسبب تحرّك عقرب الساعات، وهذا ما يذكّرنا بمفارقة زينون.
ما هو الحلّ؟
سنلجًا للمعادلات، لا تخف المعادلة بسيطة جدًا
سنفرض أنّ قياس الزاوية بين العقربين x والزمن اللازم كي تتكرّر نفس الزاوية بين العقربين للمرّة التالية مباشرةً أي خلال نفس الساعة هو t مقدّرًا بالدقائق
سنشكّل المعادلة التالية
x+6t=x+t/2+180
لا تنسَ أنّ عقرب الدقائق يتحرّك 6 درجات كلّ دقيقة، وعقرب الساعات يتحرّك نصف درجة كلّ دقيقة
t=360/11=32.72~
هل تذكر المناقشة السابقة عندما وصلنا إلى أنّه بعد دقيقتين ونصف الزائدة فوق النصف ساعة سنحتاج بضعة ثوان، لقد وصلنا إلى نفس النتيجة بالحساب الدقيق هنا.
أي أنّه كل 32.72 دقيقة (مكتوبة بالحساب المئوي، وتعادل بالحساب الستيني 32:43) سيحصل تناظر أي ستُكرّر نفس الزاوية التي كانت قبل هذا الفاصل الزمني.
لاحظ حتى الآن لم تدخل الزاوية 90 درجة في الحسابات، بالتالي يصلح هذا الحل لو كان السؤال حول أيّة زاوية كانت، والسؤالين الأكثر شيوعًا بعد سؤال التعامد هما متى ينطبق العقربان (أي يشكّلان زاوية صفر) ومتى يستقيم العقربان (أي يشكّلان زاوية 180 درجة)، لكن عند التطابق أو الاستقامة سيكون عدد الحالات نصف عدد حالات الزوايا الأخرى.
أخيرًا إلى الناتج النهائي
في يوم كامل، أي 24 ساعة، التي تعادل 1440 دقيقة
1440/360/11=44
ملحوظة1
السؤال من الأسئلة الكلاسيكية التي تختبر الانتباه، وعادةً يخطئ الكثيرون ويجيبون 48 مرة بدلًا من 44 أي بزيادة مرتين في كل 12 لأنّهم يعتقدون أنّ العقربين يشكلان زاوية قائمة مرتين كل ساعة بينما اكتشفنا بالحساب أنّهما يستغرقان أكثر من 32 دقيقة لتكرار الزاوية القائمة وهذا يعني أنّهما لن يستطيعا تشكيل زاوية قائمة مرتين خلال 60 دقيقة.
ملحوظة2
يوجد طريقة نقاش تعتمد الكلام فقط دون حسابات لكنها تبدو غير مقنعة للكثيرين، حيث نقول حتى يتمّ عقرب الساعات دورته يكون قد دار عقرب الدقائق 12 مرة، وبذلك نكون قد فقدنا دورة كاملة وهي التي كان عقرب الساعات يقضمها جزءًا تلو جزء في كلّ ساعة وبذلك فإنّ العقربين يكرران جميع الأوضاع النسبية بينهما 22 مرة كل 12 ساعة وليس 24 مرة.
ملحوظة3
بالرغم من أنّ الكلام الوارد في الفقرة السابقة قد يبدو غير مقنع إلا أنّه وبالاستعانة بالرسم البياني التالي سيبدو واضحًا، لكن مرة أخرى سنكون قد استخدمنا الحسابات وليس الكلام، الحسابات والمعادلات هنا بشكل آخر هو الخطوط البيانية.
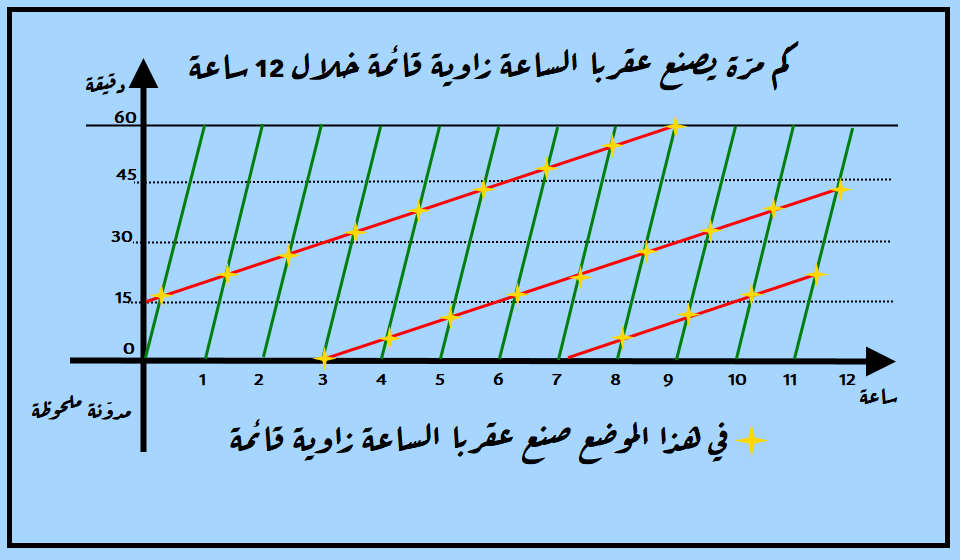
ملحوظة4
يخطئ البعض في تعليل أنّ الأوضاع النسبية للعقربين تتكرّر 22 مرة كل 12 ساعة بالقول إنّ الأوضاع النسبية تتكرّر 24 مرة لكن الساعة 3:00 والساعة 9:00 تُحسبان مرّتين ويجب حذف التكرار، وهذا خاطئ، وقد علّلنا أعلاه عدد التكرارات بالتفصيل ونزيد عليه القول حتى لو كانت هاتين الساعتين قد تكررتا مرتين فهذا يُحسب لهما لأنّ أساس السؤال مبني على حساب عدد التكرارات للزاوية المعطاة.
ملحوظة5
يمكن الحلّ بطريقة أخرى لكنها طويلة جدًا وهي اعتماد قانون حساب الزاوية بين العقربين لكن مع تعويض الزاوية 90 وإيجاد العلاقة بين الدقائق والساعات
سينتج علاقة نعوّض فيها كل القيم الممكنة للساعات من 1 الى 12 أو من 0 إلى 11

الساعة 12:49:05 تعني الساعة 12 و49 دقيقة و 5 ثوان ولا يجوز إهمال الثواني في هذه الطريقة
للتوضيح فقد حسبت الزاوية بين العقربين عند الساعة 12:49 أي بالضبط 12:49:00 وكانت كما يلي
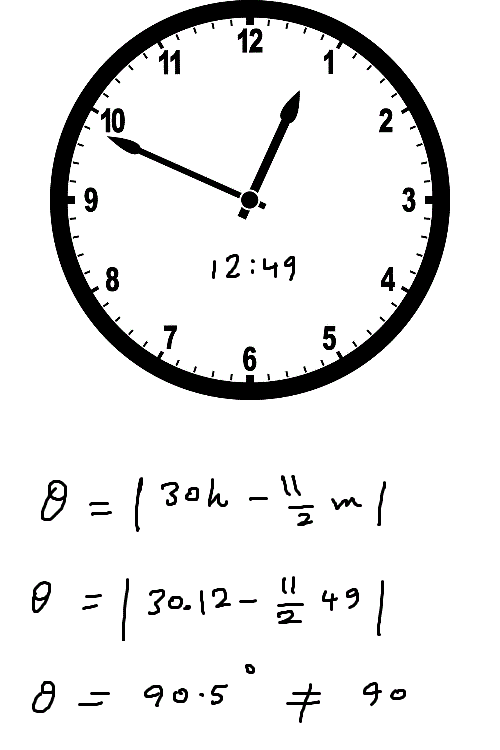
ملحوظة6
بالإضافة للقانون الوارد أعلاه يوجد موقع بل الكثير من المواقع التي تحسب لك الزاوية بمجرد إدخال قيمة الساعة مثل هذا و مثل هذا